二分图最大匹配

二分图定义（摘自wiki）\ In the mathematical field of graph theory, a bipartite graph (or bigraph) is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.\ 简单的说，如果可以将一个无向图的所有顶点分为两个集合（U和V），且任何一条边的两个顶点都不在同一个顶点集合（即一个顶点在U中，另外一个在V中），那么这个图就是二分图。\ 下图就是一个二分图的例子\

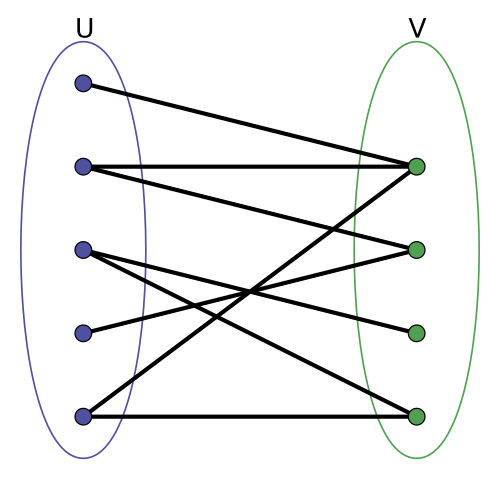
最大匹配定义\ 假设G=（V，E）是一个二分图，若存在边的集合M属于E，且M中的所有边都没有公共顶点，则称M是G的一个匹配。边数最多的匹配就是最大匹配。\ 考虑下面这个问题：\ 有男生女生两群人参加一个集体舞会，男生都希望与自己中意的女生跳舞，如何组合才能使man中满意的人数最多？\ 为了简单起见，这里设定男生为U集合，女生为V集合，且|U|=|V|=4，编号为1的男生中意1号和2号女生，编号为2的男生中意2号女生，编号为3的男生中意1号和2号女生，编号为4的男生中意3和4号女生。这个例子就是一个二分图最大匹配问题。\ \ 解决方法：\ 解决二分图最大匹配问题最常用的就是匈牙利树算法。具体流程如下：\ 1.匹配M初始化为空；\ 2.如果集合U中存在一个自由的顶点u，转到步骤3；否则，算法结束；\ 3.令r是集合U中一个自由顶点，用深度（广度）优先搜索方法，以r为根，构造一个交替路径（匹配边和未匹配边交替的路径）树T；\ 4.若T中存在一个扩展路径p（两个端点都是未覆盖点的交替路径（谢谢ccyjava指出错误）），更新匹配M；转到步骤2。\ 以上面的问题为例：\ \ 从b1点开始深度搜索，b1->g1是一条扩展路径。\ \ 从b2点开始深度搜索，b2->g1->b1->g2是一条扩展路径\ \ 从b3开始深度搜索，没有扩展路径\ \ 从b4开始深度搜索，b4->g3是一条扩展路径。

[poj1469](http://poj.org/problem?id=1469)是一个二分图最大匹配问题，下面是一个代码实例。\