最大流与最小割

最大流与最小割定义（摘自wikipedia）\ In optimization theory, the max-flow min-cut theorem states that in a flow network, the maximum amount of flow passing from the source to the sink is equal to the minimum capacity which when removed in a specific way from the network causes the situation that no flow can pass from the source to the sink.\ 最大流简单来说就是一个网络图中所能通过的最大流量，而最小割则是切断这个网络图所需的最小代价。\ 一般来说，这种网络图都一个源点（source)和一个终点（sink）。见下图（s是源点，t是终点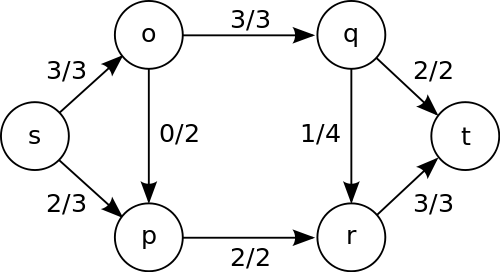）\ \ 图中，可以算出s到t的最大流量为5，切断s点发出的两条边（当然还有其他的切断方式，但最小代价是5）就能将这个网络完整阻塞。正如定义中说的那样，最大流等于最小割。

如何求最大流（最小割）\ 最常用的一类算法是Ford–Fulkerson algorithm。\ 对于一个G(V,E)来说，定义c(u,v)为u到v的容量，f(u,v)为u到v的流量。对于c(u,v)和f(u,v)来说，有以下几点特性：\ 1.f(u,v) \<= c(u,v)；\ 2.f(u,v) = -f(u,v)；\ 3.对于除掉s与t的任意一点，f(u,v1) + f(u,v2) + ... + f(u, vn) = 0。(v1...vn为V中的所有点）。\ 见下面图片的内容，剩余图中有s到t（如s->a->c->d->t）的路径，这样的路径被称为扩张路径。\ \ Ford–Fulkerson algorithm的核心就是不停地在剩余图中寻找扩张路径，直到不存在扩张路径为止。\ 算法的具体过程：\ 1.初始化各个边的流量为0，容量为输入值，网络图的最大流量为0；\ 2.建立剩余图，转下一步；\ 3.判断是否有s到t的扩张路径（bfs或dfs），如有转第4步；否则退出结束；\ 4.设扩张路径中的中的最小剩余容量为mc，则将网络图的最大流量值增加mc，并更新扩张路径上的流量值；转第2步。

以上图为例，第一次找到了s->a->b->t的扩张路径，这条路径上的最小剩余容量为c(a,b)=2，更新s->a->b->t上的每条边的流量值后，变成了上图中的上半部分。与之对应的剩余图就是下半部分图。

poj 1459就是一道最小割的题目。